流匹配：生成性人工智能的下一个前沿

==================================================

最近，Flux.ai 的 Flux 系列模型因其快速、易用（得益于扩散器）以及易于调优（同样得益于扩散器）而在技术和非技术社区中引起了广泛关注🔥。但 Flux 在图像-文本对齐和高质量生成方面的出色表现，源于一种超越标准扩散过程的新方法，称为“流匹配”。在这篇文章中，我将讨论导致流匹配的各种方法和进展🧐。

每个生成模型理想情况下都是一个密度估计器；因此，它建模一个概率密度，最终是一个联合概率分布（JPD），具有两个预期特征：采样和压缩。压缩基本上是将数据推向信息空间，这个空间看似是低维的，而采样则是从任何特征分布（z）生成 P(x|z) 的能力，这个特征分布可以是正态分布（如变分自编码器 VAE 的情况）。因此，从一个非常高的层面来看，我们试图找到一个映射/函数，将 z 映射到 x，同时也将 x 映射到 z（采样和压缩）。

假设有两个概率密度函数，一个表示为 z（潜在或可处理分布），另一个表示为 X（数据分布）。我们希望找到一个可以将 z 映射到 x 的函数，因此我们面临着 X 和 Z 之间密度的关系，这必然指出，给定 X 和 Z 是共轭分布（同一家族的分布在变换前后的关系），X 和 Z 的变化应该是相对的，因此，X 的变化是 Z 的某个函数，反之亦然。但，这个变化是由某个量缩放的。这个量由 z 和 x 之间每个维度的变化表示，由雅可比矩阵给出。在一个非常简单的层面上，它基本上是 Z 和 X 之间的变量变化。但事情并没有那么简单，因为 X 和 Z 实际上并不是共轭的，因此，我们只能依赖迭代采样和近似方法，如最优传输或吉布斯采样（在 RBM 中使用）。鉴于这些限制，大多数方法绕道而行，建模分布并近似一个不精确的映射，而像归一化流这样的算法则做出简化假设，使得计算和公式化变得可处理，形式为 p(x)dx = p(z)dz，这可以重新表述为两个项，首先是最大似然估计（MLE）项，其次是雅可比行列式。

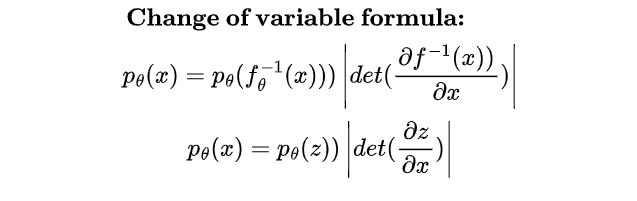
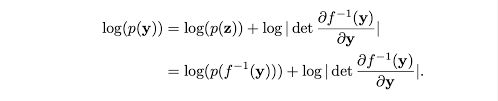
（归一化是因为变量变化总是给出一个归一化的密度函数，流则是因为它迭代地建模从源到目标的轨迹/流动）

问题从这里开始😐，要使这样的函数存在，有两个条件： 1. p(x,z) 的最大似然估计（MLE）公式必须是双射的。 2. 雅可比行列式必须能够高效计算。

为了解决这个问题，我们需要假设 z 和 X 之间状态的依赖性，使其成为双射且雅可比行列式能够高效计算，有三种主要方法（我们不会深入探讨）： 1. 耦合块：基本上将 z 分成两个部分，只有最后 k 个值预测 X 的最后 k 个值（通过均值/方差采样），X 的其他部分基本上是 z 的直接拷贝，这有什么帮助呢？因为这种方法使得雅可比矩阵变成对角矩阵，左上角（=k）变成逐元素乘积，右上角变成 0，因为 z（=k）之间没有依赖关系，因此，雅可比行列式的计算变得高效。

1. 自回归流（AR flows）是下一个逻辑扩展，不再将大 k 块处理，为什么不将每个状态/特征视为马尔可夫链的一部分，从而消除额外的依赖关系，这会导致雅可比矩阵为下三角矩阵，计算也相对简单。但这种方法保留了更多特征，并且不易受到我们在耦合层中进行特征保留的置换操作的影响。

1. 残差流，在不牺牲计算的情况下保留整个特征空间。这个想法简单却有着精美复杂的数学支持。公式为残差形式 x = z + f(z)，但这并不是双射的，因为 f 是一个神经网络。有趣的是，得益于 Banach 及其收缩映射，在理想情况下，存在一个唯一的 z，它总是映射到相同的 x（稳定状态 z），因此，这也成为双射，形式为 x = z + f(z*)，其中 f 是一个收缩映射（函数的利普希茨常数小于 1，因此，z 的变化被 X 的变化所限制）。这个形式还为我们提供了一种表示 z(k+1) 的方法，给定前一个 z(k)，这有助于我们迭代地近似 X，而不是单次框架。我们可以通过相同的公式从 z(0) 转到 z(t)，也可以反向操作，这听起来很熟悉，这大致就是扩散。至于行列式，迭代变换导致雅可比行列式的迹的无限项之和，这在全秩雅可比情况下是可怕的，但可以通过类似的矩阵公式使用 Hutchinson 方法进行迹估计。

到目前为止我们讨论的内容😃，对样本和轨迹状态（z => x）做了离散假设，为什么不将其变为连续，或者基本上是连续的残差流呢？ 残差形式 x(k+1) = x(k) + a.f(x(k)) 可以写成一个微分方程，当 k 趋向于无穷大时，这听起来熟悉吗？是的，这现在是一个神经常微分方程（ODE），但我们试图建模在 t 时刻的概率密度状态，这个状态保持不变。密度的状态变化通过连续性或传输方程建模。具体来说，从密度函数的一部分移动到另一部分的质量量可以视为原始质量与当前/移动后质量之间的散度。这个散度作为整个轨迹上的连续函数必须被积分，因此通过数值 ODE 解决，这使得其不可扩展。

这就像状态的比较，为什么不比较路径呢？ 这导致了 Flux 背后的方法，称为流匹配。这个想法大致是这样的……我们从一个非常简单的分布开始，并将其移动到预期的分布，但由于我们不知道预期的分布，我们通过迭代扰动来对其进行条件化，并估计已知的添加噪声，最终建模潜在分布，这个过程被简单地称为条件流匹配。理论上证明，在理想条件下，条件目标和无条件目标是完全相同的，因此，通过优化 CFM，我们倾向于优化流匹配背后的主要目标。

这正是扩散过程，但主要的区别在于边界条件或初始和最终状态的定义，扩散过程假设纯噪声为 z(t)，数据为 z(0)，但这是在 t 趋向于无穷大的假设下。然而，这在经验上是不可行的，相反，我们在足够的时间戳内执行此操作，因此，我们保持在一个更浅的流形中，并且速度也较慢（后面由 LCMs 处理），这就像在低分辨率地图中寻找方向，而在流匹配中，纯噪声和数据空间被建模为线性插值（lerp），形式为 x(t) = tx(t-1) + (1-t)x(0)，因此，在 t=0 时我们处于纯数据样本，而在 t=t 时我们处于纯噪声，这提供了一个更精细的状态/流形进行建模，因此，更具代表性和高分辨率的地图，也称为条件流匹配（通过噪声分布进行条件化）。

流匹配无疑是一个独特而直观的想法，预计将受到研究人员的广泛关注，基于此的产品将为消费者市场带来启示。我的解释远未达到该主题的实际深度和广度，因此，需要更全面和技术性的深入探讨，但我希望这些术语/关键词能为主题之间提供一个构建块和中介连接。

您可以在这里找到论文：https://arxiv.org/abs/2210.02747
有用的论文（残差流）：https://arxiv.org/abs/1906.02735
特别博客文章：https://lilianweng.github.io/posts/2018-10-13-flow-models/
有用的博客文章：https://jmtomczak.github.io/blog/18/18_fm.html

今天就到这里。
关注我以获取更多有见地的文章，祝您学习愉快，再见。👋