什么是 DiTsDiTs（动态图像转换）？

扩散变换器（Diffusion Transformers）是图像生成的新范式，它们为像 SD3 和 Flux 这样的模型提供了多模态扩散变换器的基础。然而，似乎缺乏高质量的参考资源，因此我希望这对你和我未来的参考都能有所帮助。

由于扩散变换器的根源来自视觉变换器（Vision Transformers），因此最好先快速而清晰地理解一下视觉变换器。

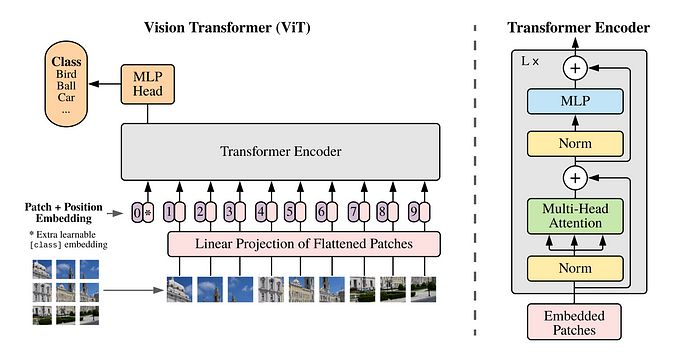
图1：视觉变换器编码器的示意图

自从论文《Attention is all you need》发布以来，视觉领域的研究工作数量增加了。视觉变换器采用了一种基本的方法：

1. 首先，它们将图像转换为多个补丁，暂且考虑 4 个补丁，由于图像有 3 个通道，因此输入大小为：补丁数量 * (通道数 * 补丁高度 * 补丁宽度)。这些数据被投影到 D 维向量空间。位置嵌入被添加以存储与图像中像素位置相关的信息。添加了一个 CLS 令牌，稍后将用于获取分类分数。
2. 然后是我们的聪明朋友——注意力（Attention），它帮助理解像素之间的关系，这通过多头注意力（Multi Head Attention）实现，这本身就是一个值得深入探讨的主题。我们将在后面的部分提到这一点。
3. MLP 是单个视觉变换器块的最后一层，在这三者之间是层归一化（Layer Norm），它有助于获得更平滑的梯度流，并且在训练期间也有利于多头注意力的稳定性。因此，我们连接 N 层视觉变换器块，并在每个块和层归一化之后存在残差连接。

这不是视觉变换器的课程，而是扩散变换器！为什么要提到它呢？因为如果你理解了视觉变换器，你就知道了扩散变换器工作原理的 70%。

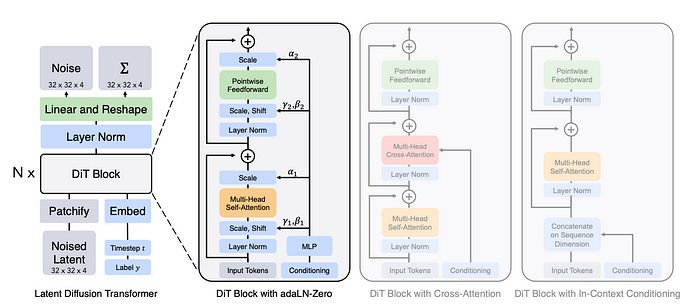
图2：扩散变换器（DiT）架构。左侧是正在训练的潜在 DiT 模型，右侧是稍后将在本文中解释的 DiT 块的细节。 :)

与常规扩散模型一样，扩散变换器需要变分自编码器（VAE）来对图像进行编码和解码，从像素到潜在空间，反之亦然。

暂且考虑整个 DiT 是一个带有 VAE 的视觉变换器，最后一层输出 D 维的嵌入，并将其转换为 (通道数 * 补丁高度 * 补丁宽度) 的潜在补丁。

输出的潜在数据随后通过预训练的 VAE 解码器解码到像素空间，以便我们可以获得高分辨率的像素图像。

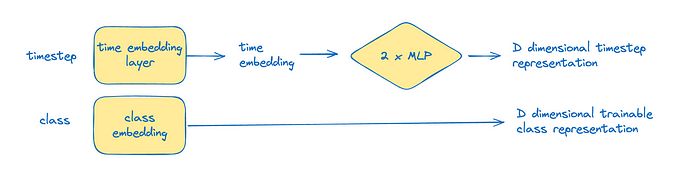
图3：时间步和类别表示

简单来说，扩散是一个去噪过程，它也需要一些时间步信息。这是通过一个嵌入层和 2 个 MLP 层将其投影到 D 维空间来实现的。类别表示是可训练的，它也被投影到该维度。

现在让我们深入探讨图2的 DiT，并稍微剖析一下。作者提出了 2 种变体，具体如下：

1. 上下文条件——简单地说，时间步和类别嵌入作为两个额外的令牌被添加，在去补丁化（un-patchify）块之前，我们将去掉这些令牌，并处理剩余的令牌。
2. 交叉注意力——在这个变体中，在多头注意力和 MLP 之间添加了一个交叉注意力层，使其能够关注类别嵌入和时间步表示。
3. 自适应层归一化——在这里，时间步嵌入与类别嵌入相加，经过一个 MLP 层，投影到 4 个 D 维的仿射参数。这些参数作为前向传播时权重的幅度和偏移的 β 和 γ。
4. 自适应层归一化零——这添加了额外的 2 个 D 维参数，以确保在残差连接之前我们需要乘以的缩放因子 α。

缩放因子最初设置为零，以确保在开始时是一个恒等块（输出与输入相同），以确保更好的训练和梯度。

根据 DiT 的缩放，我们都知道，随着计算和参数数量的增加，质量会越来越好。这在这里同样适用。官方论文中有这些模型配置，包括层数、维度和头数。

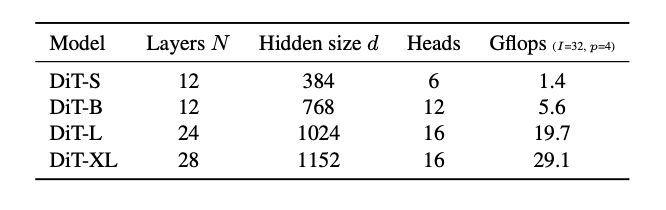
图4：DiT 的缩放、模型配置，包括小型（S）、基础（B）、大型（L）和超大型（XL）变体的详细信息

不仅如此，保持模型参数不变，发现补丁大小越小（或图像的补丁数量越多），图像质量会越来越好。

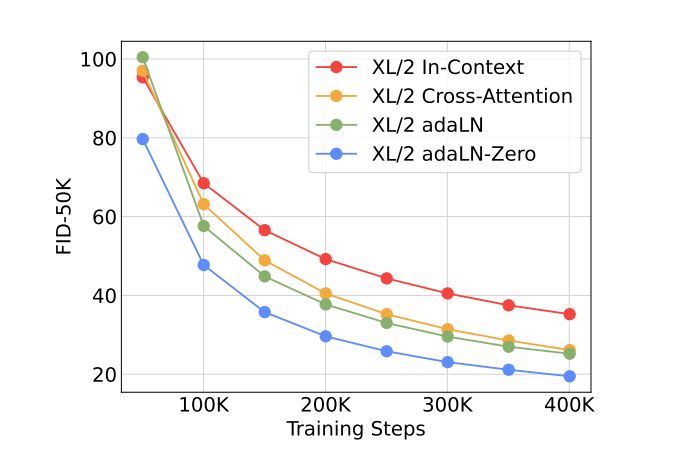
图5：不同条件策略的 FID-50k 比较——越低越好

随着计算量的增加，我们在 DiT 中获得了更好的性能。本文中训练的最大模型是补丁大小为 2 的 DiT XL，它生成的图像质量非常高，FID 分数甚至低于潜在扩散模型。

哇！有很多内容需要消化，慢慢来，放松一下。现在让我们从头开始实现 DiT。

首先实现提取补丁和重建图像的函数，由于我没有 GPU，请不要介意我在补丁大小为 8 的情况下进行训练，且实现将采用自适应层归一化。

def extract_patches(image_tensor, patch_size=8):
    """
    从图像张量中提取补丁。

    参数：
        image_tensor (torch.Tensor): 输入图像张量，形状为 (bs, c, h, w)。
        patch_size (int, optional): 要提取的补丁大小。默认为 8。

    返回：
        torch.Tensor: 提取的补丁，形状为 (bs, L, c * patch_size * patch_size)，
                      其中 L 是补丁的数量。
    """
    bs, c, h, w = image_tensor.size()

    unfold = torch.nn.Unfold(kernel_size=patch_size, stride=patch_size)
    unfolded = unfold(image_tensor)

    unfolded = unfolded.transpose(1, 2).reshape(bs, -1, c * patch_size * patch_size)
    return unfolded

def reconstruct_image(patch_sequence, image_shape, patch_size=8):
    """
    从补丁序列重建原始图像张量。

    参数：
        patch_sequence (torch.Tensor): 补丁序列，形状为 (bs, L, c * patch_size * patch_size)。
        image_shape (tuple): 原始图像张量的形状 (bs, c, h, w)。
        patch_size (int, optional): 提取时使用的补丁大小。默认为 8。

    返回：
        torch.Tensor: 重建的图像张量，形状为 (bs, c, h, w)。
    """
    bs, c, h, w = image_shape
    num_patches_h = h // patch_size
    num_patches_w = w // patch_size
    
    unfolded_shape = (bs, num_patches_h, num_patches_w, patch_size, patch_size, c)
    patch_sequence = patch_sequence.view(*unfolded_shape)
    
    patch_sequence = patch_sequence.permute(0, 5, 1, 3, 2, 4).contiguous()
    
    reconstructed = patch_sequence.view(bs, c, h, w)
    
    return reconstructed

现在是时候制作条件层归一化，它根据时间和类别嵌入的仿射参数来缩放层归一化（在这个实现中仅使用时间嵌入）。

import torch.nn as nn

class ConditionalNorm2d(nn.Module):
    """
    用于 2D 输入的条件层归一化模块。

    该模块应用层归一化，然后根据输入特征缩放和偏移归一化的输入。

    参数：
        hidden_size (int): 要归一化的隐藏维度的大小。
        num_features (int): 条件输入的特征数量。

    属性：
        norm (nn.LayerNorm): 层归一化模块。
        fcw (nn.Linear): 用于生成缩放因子的线性层。
        fcb (nn.Linear): 用于生成偏移因子的线性层。
    """

    def __init__(self, hidden_size, num_features):
        super(ConditionalNorm2d, self).__init__()
        self.norm = nn.LayerNorm(hidden_size, elementwise_affine=False)
        self.fcw = nn.Linear(num_features, hidden_size)
        self.fcb = nn.Linear(num_features, hidden_size)

    def forward(self, x, features):
        """
        ConditionalNorm2d 模块的前向传播。

        参数：
            x (torch.Tensor): 形状为 (batch_size, sequence_length, hidden_size) 的输入张量。
            features (torch.Tensor): 形状为 (batch_size, num_features) 的条件特征。

        返回：
            torch.Tensor: 与输入 x 形状相同的归一化和条件输出张量。
        """
        bs, s, l = x.shape
        
        out = self.norm(x)
        w = self.fcw(features).reshape(bs, 1, -1)
        b = self.fcb(features).reshape(bs, 1, -1)

        return w * out + b

现在让我们实现变换器块，并将上述所有类整合到主 DiT 块中。

import torch
import torch.nn as nn
from sinusoidal_pos_emb import SinusoidalPosEmb
from patch_utils import extract_patches, reconstruct_image
from conditional_norm2d import ConditionalNorm2d

class TransformerBlock(nn.Module):
    """
    带有自注意力和条件归一化的变换器块。

    参数：
        hidden_size (int): 隐藏维度的大小。默认为 128。
        num_heads (int): 注意力头的数量。默认为 4。
        num_features (int): 条件归一化的特征数量。默认为 128。

    属性：
        norm (nn.LayerNorm): 输入的层归一化。
        multihead_attn (nn.MultiheadAttention): 多头注意力机制。
        con_norm (ConditionalNorm2d): 条件归一化层。
        mlp (nn.Sequential): 用于特征处理的多层感知机。
    """

    def __init__(self, hidden_size=128, num_heads=4, num_features=128):
        super(TransformerBlock, self).__init__()
        
        self.norm = nn.LayerNorm(hidden_size)
        self.multihead_attn = nn.MultiheadAttention(hidden_size, num_heads=num_heads, 
                                                    batch_first=True, dropout=0.0)
        self.con_norm = ConditionalNorm2d(hidden_size, num_features)
        self.mlp = nn.Sequential(
            nn.Linear(hidden_size, hidden_size * 4),
            nn.LayerNorm(hidden_size * 4),
            nn.ELU(),
            nn.Linear(hidden_size * 4, hidden_size)
        )
                
    def forward(self, x, features):
        """
        TransformerBlock 的前向传播。

        参数：
            x (torch.Tensor): 输入张量。
            features (torch.Tensor): 用于归一化的条件特征。

        返回：
            torch.Tensor: 经过注意力和 MLP 层处理后的张量。
        """
        norm_x = self.norm(x)
        x = self.multihead_attn(norm_x, norm_x, norm_x)[0] + x
        norm_x = self.con_norm(x, features)
        x = self.mlp(norm_x) + x
        return x

class DiT(nn.Module):
    """
    用于视觉编码的扩散变换器（DiT）模块。

    参数：
        image_size (int): 输入图像的大小（假设为正方形图像）。
        channels_in (int): 输入通道的数量。
        patch_size (int): 图像补丁的大小。默认为 16。
        hidden_size (int): 隐藏维度的大小。默认为 128。
        num_features (int): 时间嵌入的特征数量。默认为 128。
        num_layers (int): 变换器层的数量。默认为 3。
        num_heads (int): 每个变换器块中的注意力头数量。默认为 4。

    属性：
        time_mlp (nn.Sequential): 用于时间步嵌入的 MLP。
        patch_size (int): 图像补丁的大小。
        fc_in (nn.Linear): 用于补丁嵌入的线性层。
        pos_embedding (nn.Parameter): 可学习的位置嵌入。
        blocks (nn.ModuleList): 变换器块模块的列表。
        fc_out (nn.Linear): 输出投影的线性层。
    """

    def __init__(self, image_size, channels_in, patch_size=16, 
                 hidden_size=128, num_features=128, 
                 num_layers=3, num_heads=4):
        super(DiT, self).__init__()
        
        self.time_mlp = nn.Sequential(
            SinusoidalPosEmb(num_features),
            nn.Linear(num_features, 2 * num_features),
            nn.GELU(),
            nn.Linear(2 * num_features, num_features),
            nn.GELU()
        )
        
        self.patch_size = patch_size
        self.fc_in = nn.Linear(channels_in * patch_size * patch_size, hidden_size)
        
        seq_length = (image_size // patch_size) ** 2
        self.pos_embedding = nn.Parameter(torch.empty(1, seq_length, hidden_size).normal_(std=0.02))
        
        self.blocks = nn.ModuleList([
            TransformerBlock(hidden_size, num_heads) for _ in range(num_layers)
        ])
        
        self.fc_out = nn.Linear(hidden_size, channels_in * patch_size * patch_size)
                
    def forward(self, image_in, index):
        """
        DiT 模块的前向传播。

        参数：
            image_in (torch.Tensor): 输入图像张量。
            index (torch.Tensor): 时间步索引张量。

        返回：
            torch.Tensor: 处理后的图像张量。
        """
        index_features = self.time_mlp(index)

        patch_seq = extract_patches(image_in, patch_size=self.patch_size)
        patch_emb = self.fc_in(patch_seq)

        embs = patch_emb + self.pos_embedding
        
        for block in self.blocks:
            embs = block(embs, index_features)
        
        image_out = self.fc_out(embs)
        
        return reconstruct_image(image_out, image_in.shape, patch_size=self.patch_size)

现在我们要引入来自 DDIM 论文的老朋友，这个术语帮助我们在扩散过程中从第一步开始以非常确定的方式添加噪声。

α 的累积乘积是所有 α 的乘积，表示图像中剩余的原始图像的数量，而 β 是随着时间步的推进你添加到图像中的高斯噪声的数量。

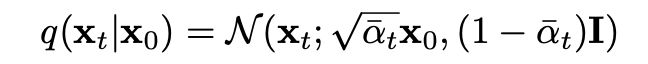
图6：给定时间 t 的像素的条件概率，考虑其在时间 0 的噪声

在这里我们将实现这个功能。

import torch
from tqdm import trange
import copy

def noise_from_x0(curr_img, img_pred, alpha):
    """
    计算当前图像及其预测的噪声。

    参数：
        curr_img (torch.Tensor): 当前图像。
        img_pred (torch.Tensor): 预测的图像。
        alpha (float): 扩散过程的 alpha 值。

    返回：
        torch.Tensor: 计算得到的噪声。
    """
    return (curr_img - alpha.sqrt() * img_pred) / ((1 - alpha).sqrt() + 1e-4)

def cold_diffuse(diffusion_model, sample_in, total_steps, start_step=0):
    """
    对输入样本执行冷扩散。

    参数：
        diffusion_model (torch.nn.Module): 要使用的扩散模型。
        sample_in (torch.Tensor): 要扩散的输入样本。
        total_steps (int): 扩散步骤的总数。
        start_step (int, optional): 从哪个步骤开始扩散。默认为 0。

    返回：
        torch.Tensor: 扩散后的输出图像。
    """
    diffusion_model.eval()
    bs = sample_in.shape[0]
    device = sample_in.device
    alphas = torch.flip(cosine_alphas_bar(total_steps), (0,)).to(device)
    random_sample = copy.deepcopy(sample_in)

    with torch.no_grad():
        for i in trange(start_step, total_steps - 1):
            index = (i * torch.ones(bs, device=device)).long()

            img_output = diffusion_model(random_sample, index)

            noise = noise_from_x0(random_sample, img_output, alphas[i])
            x0 = img_output

            rep1 = alphas[i].sqrt() * x0 + (1 - alphas[i]).sqrt() * noise
            rep2 = alphas[i + 1].sqrt() * x0 + (1 - alphas[i + 1]).sqrt() * noise

            random_sample += rep2 - rep1

        index = ((total_steps - 1) * torch.ones(bs, device=device)).long()
        img_output = diffusion_model(random_sample, index)

    return img_output

太好了！你已经完成了，稍等一下，我将向你展示可能性。虽然你已经成为了 DiT 专家，但为什么不再提升到专家级别呢？

是时候训练我们的模型了，我们使用 Adam 作为优化器，使用 L1 损失进行噪声预测，并初始化模型进行训练。

dit = DiT(latent_size, channels_in=latents.shape[1], patch_size=patch_size, 
          hidden_size=768, num_layers=10, num_heads=8).to(device)

optimizer = optim.Adam(dit.parameters(), lr=lr)

alphas = torch.flip(cosine_alphas_bar(timesteps), (0,)).to(device)

dit.train()
for epoch in pbar:
    pbar.set_postfix_str('Loss: %.4f' % (mean_loss/len(train_loader)))
    mean_loss = 0

    for num_iter, (latents) in enumerate(tqdm(train_loader, leave=False)):
        latents = latents.to(device)
        
        # 当前小批量的大小
        bs = latents.shape[0]

        rand_index = torch.randint(timesteps, (bs, ), device=device)
        random_sample = torch.randn_like(latents)
        alpha_batch = alphas[rand_index].reshape(bs, 1, 1, 1)
        
        noise_input = alpha_batch.sqrt() * latents +
        (1 - alpha_batch).sqrt() * random_sample
        
        with torch.cuda.amp.autocast():
            latent_pred = dit(noise_input, rand_index)
            loss = F.l1_loss(latent_pred, latents)
        
        # 反向传播
        optimizer.zero_grad()
        scaler.scale(loss).backward()
        scaler.step(optimizer)
        scaler.update()
        
        # 记录生成器训练损失
        loss_log.append(loss.item())
        mean_loss += loss.item()

    # 每个 epoch 快速保存模型
    torch.save({'epoch': epoch + 1,
                'train_data_logger': loss_log,
                'model_state_dict': dit.state_dict(),
                'optimizer_state_dict': optimizer.state_dict(),
                 }, "latent_dit.pt")

plt.plot(loss_log[1000:])

当我们在 1000 次迭代后绘制损失时，经过一百万次训练可能需要几天，但你不需要等那么久，可以直接从 HF 拉取权重。

图7：1000 次迭代后的损失日志

让我们看看我们自定义训练的扩散变换器的表现，生成 8 个随机噪声样本，让扩散变换器从这些图像中采样，我很好奇结果如何。

latent_noise = 0.95 * torch.randn(8, 4, latent_size, latent_size, device=device)
with torch.no_grad():
    with torch.cuda.amp.autocast():
        fake_latents = cold_diffuse(dit, latent_noise, total_steps=timesteps)
        fake_sample = vae.decode(fake_latents / 0.18215).sample

plt.figure(figsize = (20, 10))
out = vutils.make_grid(fake_sample.detach().float().cpu(), nrow=4, normalize=True)
_ = plt.imshow(out.numpy().transpose((1, 2, 0)))

图8：这些 AI 图像可能会接管我们的社会

天哪！我不敢相信这些是通过训练一个简单的扩散变换器生成的。可能性是？无穷无尽的！

图像到图像是一个有趣的工作流程，在这里，我们可以从通过前向过程添加噪声的图像开始，并将其用作生成的起点！我们添加的噪声越多，生成的图像与源图像的距离就越远！

with torch.no_grad():
    with torch.cuda.amp.autocast():
        latents = vae.encode(test_tensor).latent_dist.sample().mul_(0.18215)
        latents = latents.expand(mini_batch_size, 4, latent_size, latent_size)
        latent_noise = 0.95 * torch.randn_like(latents)

        alpha_batch = alphas[index].expand(mini_batch_size).reshape(mini_batch_size, 
                                                                    1, 1, 1)
        noise_input = alpha_batch.sqrt() * latents +
        (1 - alpha_batch).sqrt() * latent_noise
        
        fake_latents = cold_diffuse(dit, noise_input, 
                                    total_steps=timesteps, 
                                    start_step=index)
        
        fake_sample = vae.decode(fake_latents / 0.18215).sample

结果？在这里！

图9：奥巴马会喜欢这些生成的图像

另一个很好的实现可以是图像的修复，即在源图像的特定部分进行绘制（生成）。

为此，我们需要更新我们的扩散生成循环，以包含目标图像（或潜在图像）和“掩码”。这个“掩码”在最简单的形式中是一个二进制（1 和 0），定义了我们希望保留图像的哪个部分，以及我们希望移除哪个部分！

def cold_diffuse_inpaint(diffusion_model, sample_in, target, mask, total_steps, start_step=0):
    """
    对输入样本执行冷扩散修复。

    此函数在应用冷扩散过程时结合目标图像和修复掩码。

    参数：
        diffusion_model (torch.nn.Module): 要使用的扩散模型。
        sample_in (torch.Tensor): 要扩散的输入样本。
        target (torch.Tensor): 用于修复的目标图像。
        mask (torch.Tensor): 指示要修复的图像部分的掩码。
        total_steps (int): 扩散步骤的总数。
        start_step (int, optional): 从哪个步骤开始扩散。默认为 0。

    返回：
        torch.Tensor: 修复后的输出图像。
    """
    diffusion_model.eval()
    bs = sample_in.shape[0]
    device = sample_in.device
    alphas = torch.flip(cosine_alphas_bar(total_steps), (0,)).to(device)
    random_sample = copy.deepcopy(sample_in)
    
    with torch.no_grad():
        for i in trange(start_step, total_steps - 1):
            index = (i * torch.ones(bs, device=device)).long()

            noisy_target = alphas[i].sqrt() * target + 
                           (1 - alphas[i]).sqrt() * torch.randn_like(target)
                
            random_sample = mask * random_sample + (1 - mask) * noisy_target
            
            img_output = diffusion_model(random_sample, index)

            noise = noise_from_x0(random_sample, img_output, alphas[i])
            x0 = img_output

            rep1 = alphas[i].sqrt() * x0 + (1 - alphas[i]).sqrt() * noise
            rep2 = alphas[i + 1].sqrt() * x0 + (1 - alphas[i + 1]).sqrt() * noise
            
            random_sample += rep2 - rep1
            
        index = ((total_steps - 1) * torch.ones(bs, device=device)).long()
        img_output = diffusion_model(random_sample, index)

    return img_output


with torch.no_grad():
    with torch.cuda.amp.autocast():
        latents = vae.encode(test_tensor).latent_dist.sample().mul_(0.18215)
        latents = latents.expand(mini_batch_size, 4, latent_size, latent_size)
        noise_input = 0.9 * torch.randn_like(latents)

        fake_latents = cold_diffuse_inpaint(dit, 
                                            noise_input, 
                                            total_steps=timesteps,
                                            target=latents,
                                            mask=mask)
        
        fake_sample = vae.decode(fake_latents / 0.18215).sample

由于我们没有生成任何平滑的掩码，且选择的补丁大小和模型也不理想，因此图像的效果并不那么理想。我们还可以尝试反转掩码。

图10：奥巴马在平行宇宙中（开玩笑，只是不同的外观）

让我们反转掩码，看看这些图像的背景能产生多少多样性。这可能会非常有趣。

图11：奥巴马的不同角色

等等，事情还没有结束，你可以结合文本条件与交叉注意力层，这可能会使你的图像生成更加多样化。

以下是 PixArt α 如何实现他们的第一个扩散变换器与文本条件的示例，增加了额外的多头交叉注意力层。

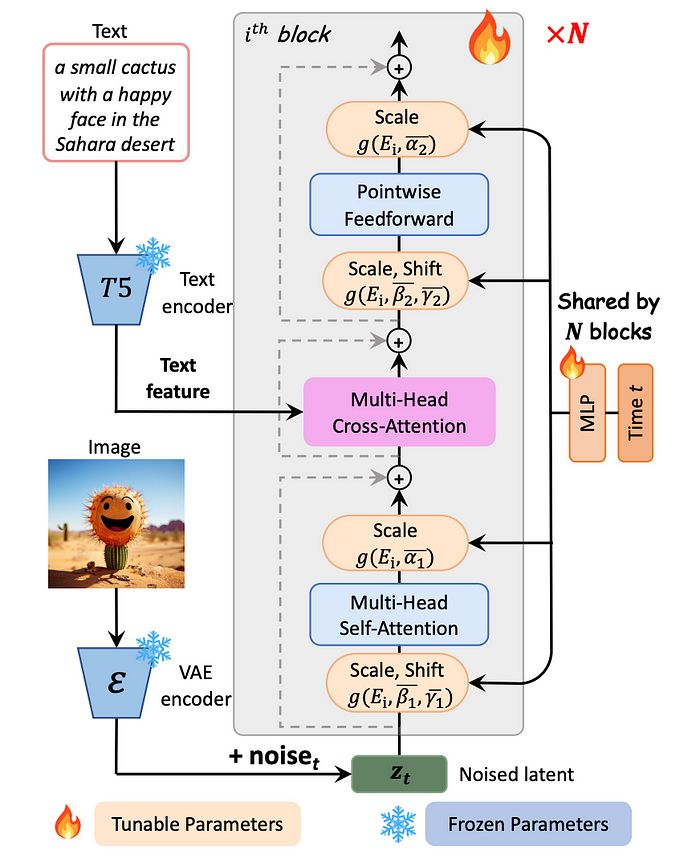
图12：PIXART-α 的模型架构。每个块中集成了交叉注意力模块，以注入文本条件。

并不是所有的代码都在这篇文章中分享，我参考了以下文献，并主要从中获得灵感，尤其是扩散的理论。有关详细实现，请参考 这个。

所以你真的成为了 DiT 专家了吧！别忘了分享这篇博客，写这整个实现花了我整整一周的时间，都是为了你。

请支持我，分享给你的朋友们！下次深度探讨再见 :）

参考文献：

1. https://github.com/chuanyangjin/fast-DiT
2. https://github.com/facebookresearch/DiT
3. https://arxiv.org/pdf/2212.09748
4. https://www.youtube.com/watch?v=aSLDXdc2hkk&t=1322s
5. https://www.youtube.com/watch?v=tU_ix9UU-g0&t=16s
6. https://arxiv.org/pdf/2310.00426